What is gravity?#

---

We experience gravity as a force pulling objects with mass toward the center of the Earth. It may be somewhat surprising that, despite treating gravity as a force in physics, it is actually the basic geometry of space-time in the presence of matter - the three dimensional surface, with influence on time, surrounding any object with mass.

We will examine this idea of gravity as geometry later. But first, let's examine gravity as a force. We consider gravity to be one of the four fundamental forces of the universe. It is also the weakest.

Newton's law of universal gravitation#

---

\(F_g=\frac{GMm}{r^2}\)

...where G is the gravitational constant \(6.6743\times 10^{-11}\;\frac{m^3}{kg\cdot s^2}\), and where M and m are masses of two bodies, r is the distance between the centers of the two masses, and \(F_g\) is the gravitational force between them in Newtons.

Breaking apart this equation into fundamental units, you can observe that gravity is a force.

\(F_g=\frac{GMm}{r^2}=\frac{G\cdot kg^2}{m^2}, G=\frac{m^3}{kg\cdot s^2}\)

\(F_g=\frac{m^3 \cdot kg^2}{kg\cdot s^2 \cdot m^2}\)

\(F_g=\frac{m \cdot kg}{ s^2}\)

\(F_g=kg\cdot \frac{m}{s^2}\)

\(F_g=mass \cdot acceleration\)

The fact that Newton's law of universal gravitation is consistent with Newton's second law, \(F=ma\), is not at all surprising. And it allows us predict the effect of gravity on objects.

Falling objects#

---

The Earth has a mass of approximately \(5.972 \times 10^{24}\;kg\). A 16 cm bowling ball has a mass of approximately \(2.85\;kg\). Dropping a bowling ball from a 30 meter platform yields the following data:

time s	displacement m	velocity ms^-1	acceleration ms^-2
0.000	0.000	0.000
0.250	0.306	2.452	9.807
0.500	1.226	4.903	9.807
0.750	2.758	7.355	9.807
1.000	4.903	9.807	9.807
1.250	7.661	12.258	9.807
1.500	11.032	14.710	9.807
1.750	15.016	17.162	9.807
2.000	19.613	19.613	9.807
2.250	24.823	22.065	9.807
2.474	30.000	24.262	9.807

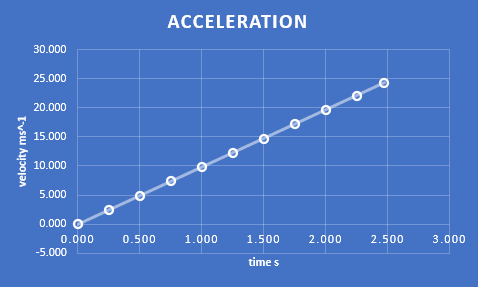
On the graph above, each point is a velocity at a given time. The slope between any two of these points provides acceleration. Notice that regardless of which two points are chosen, the acceleration is constant at approximately \(9.81 \frac{m}{s^2}\). The easiest place to see and estimate the slope are the points at approximately 10 and 20 m/s at 1 and 2 seconds - a move of ~10 m/s in one second.

It turns out that this acceleration due to gravity is virtually constant everywhere on Earth for all objects, where air resistance is negligible. There are some differences depending upon your coordinates, but the variations are small, ranging from about 9.78 to 9.83 \(\frac{m}{s^2}\) The variation is due to variable distances to the center of the Earth at different latitudes. The distance r is inversely proportional to the acceleration due to gravity g.

Going back to our definition of force (F=ma), if our acceleration is \(~9.81 ms^{-2}\) for all falling objects on Earth, then we need only multiply by the mass to determine the force of gravity on that object.

\(F=ma\)

\(F=2.85 \cdot 9.81\)

\(F=27.96 N\)

Pulling up the Earth#

---

The identical force is also exerted upon the Earth. Remember that in Newton's law of universal gravitation, the force of gravity applies to both M and m, the larger M being the Earth in this scenario. Therefore, what is the resulting upward acceleration of the Earth in response to the falling bowling ball? Not much, to be sure.

\(F=ma\)

\(27.96=5.972\times 10^{24} \cdot a\)

\(a=\frac{27.96}{5.972\times 10^{24}}=4.68\times 10^{-24}\)

\(a=0.00000000000000000000000468 N\)

This is an absurdly small force, easily overriden by measuring errors and other forces - and irrelevant for most purposes except to demonstrate that both massive objects experience the force of gravity.

How well does Newton's law of universal gravitation match our gravitational force measurement of 27.96 Newtons? The average radius of the Earth is 6,371,000 meters. If we drop the bowling ball from 6,371,030 meters above the Earth's core, we can express gravity as follows:

\(F_g=\frac{GMm}{r^2}\)

\(F_g=\frac{6.6743 \times 10^{-11} \cdot 5.972 \times 10^{24} \cdot 2.85}{6,371,030^2}\)

\(F_g=27.97 N\)

Not a bad match, considering the gross liberties we are taking with the distance measurements for r.

Determining the value of g#

---

Another way to look a this, is that the gravitational constant of ~9.81 (let's call it g) is the acceleration part of F=ma

\(F_g=mg\)

\(F_g=\frac{GMm}{r^2} \therefore\)

\(mg=\frac{GMm}{r^2}\)

\(g=\frac{GM}{r^2}\)

Two things equal to the same thing are equal to one another, so we can set our two force equations equal to one another and solve for g. Notice the small m cancels out, leaving us with an equation to determine the acceleration due to gravity for any massive body (star, planet, moon, etc).

What would you weigh on the Moon?#

---

For instance, the value of g for the Moon is:

\(g=\frac{6.67\times 10^{-11}\cdot 7.35\times 10^{22}}{1,737,400}\)

\(g=1.63 \frac{m}{s^2}\)

Comparing that acceleration to the g of Earth, we find that the ratio is 1:6. Therefore, the Moon has only one sixth the gravity of the Earth. For example, an adult male of 88 kg would experience a gravitational force of:

\(F=mg\)

\(F=88\cdot 1.63\)

\(F= 143.44\;N\)

On the Earth, that same force would correspond to:

\(F=mg\)

\(143.44=m\cdot 9.81\)

\(m=\frac{143.44}{9.81}\)

\(m=14.62\;kg\)

Of course, your mass would remain 88 kg. But the force exerted on you by the Moon would feel the same as if your mass was only 14.62 kg on the Earth. This would allow you to lift heavy objects, jump higher, and in longer arcs - and perform what would be considered superhuman feats if you were on Earth.

Gravity as geometry#

---

For all its utility and precision, Newton's equations are ultimately incomplete. Einstein discovered that time was not the universal constant that Newton believed it to be, but changes relative to rate of movement and mass.

Imagine a vertical line of observation sensors stacked upon a solid spherical body with the mass of the Sun. The distance from the center of the Sun-like sphere to any sensor can be defined by r+h, where r is the radius of the sphere and h is the sensor's distance from the surface. We have already learned that the value of g depends upon the distance from the body, so we can express the change in g as follows:

\(g(h)=\frac{GM}{(r+h)^2}\)

We can see that the acceleration due to gravity g is inversely proportional to the distance from the surface of the body h. As we move away from the large object, our acceleration toward the object lessens. We can think of this as decreasing gravitational pull with distance.

We can then use this value in the following relationship:

\(T=\exp\left[\frac{1}{c^2}\int_{0}^h \frac{GM}{(r+h)^2}\right]\)

It looks intimidating, but it is quite straightforward. We integrate the acceleration due to gravity g by distance from the surface h, meaning we sum all the g values from the surface to some distance we designate. Then we divide that value by the speed of light squared \(c^2\). Finally, we use this value as the exponent to the constant e. This will tell us the gravitational time dilation ratio for that distance.

The local time is calculated from the surface of the body, so any calculated time dilation applies to a sensor at distance h. For instance, if T=1.25 then 1.25 seconds pass at distance h for each second that passes on the surface. In other words, the time on the surface is moving more slowly than at h.

Time flows slower on the Sun#

---

However, the effect is not nearly so pronounced. If we produce a table for increasing distances h and watch T change, you'll notice that at a certain point, T effectively stops changing. This is the point where mass of the body no longer substantially influences the flow of time.

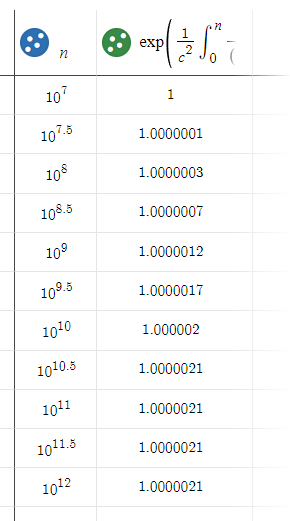
In our example of a sphere with the mass of the Sun, the time dilation ratio is too small to be calculated by my software at \(10^7\) meters, and increases to 1.0000021 at \(10^{10.5}\) meters before remaining essentially constant. I used the decimal exponents for convenience. The distance \(10^{10.5}\) is the same as \(3.16\times 10^{10}\) meters. This is about one fifth of 1 AU (the distance from the Sun to the Earth). Clearly, there is significant gravity here, but not enough to influence time significantly. The effect has fallen off.

The ratio at 1 AU is still 1.0000021, so we can use this to determine the difference between the flow of time on Earth, relative to the Sun. On Earth, we experience 1.0000021 seconds to every second on the Sun. We can restructure this difference into seconds per year:

\(s=(365\cdot 24\cdot 3600)-\left[\frac{(365\cdot 24\cdot 3600)}{1.0000021}\right]=66.225\)

In other words, after one Earth-year, a clock on the surface of the Sun would be 66 seconds behind a clock on the Earth, due to the effect of gravitational time dilation.

Space-time curvature#

---

Here is the link demonstrating the effect in desmos:

Notice the shape of the curve. Time dilation quickly rises and reaches a point where further expansion is very limited. One way to look at this is like a space-time gravity well, with the surface of the Sun at (0,1). If you can mentally rotate this shape around the y-axis you can see that it forms a 3D well or pit shape. The higher surface of this shape represents time flowing outside the gravitational influence of the Sun. If you can further mentally rotate this well around the sphere of the Sun in every direction, like a cloth polishing a bowling ball from each direction, you can visualize the effect of matter on time.