Orbit of Halley's Comet#

We will model one of the most well-known comets in the solar system: Halley's Comet, officially designated 1P/Halley.

To do this, we will parametrize the equation for an ellipse, and use three measured values, perihelion, aphelion, and eccentricity, to calculate the orbital axes, the foci of the ellipse, and the period. We will then model the orbit by incrementing the parameter \(t\) from \(0\) to \(2\pi\) radians.

Ellipses#

An ellipse has two foci (singular focus). One way to visualize the need for two foci is to hammer two nails into a board, place a looped string over the nails with some slack, and use the string, pulled taught, to draw a shape by pulling to the extremes of the string loop. The foci determine the qualities of the ellipse that is drawn.

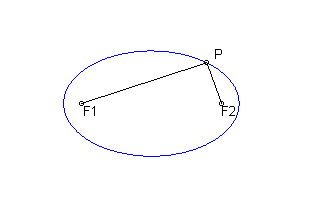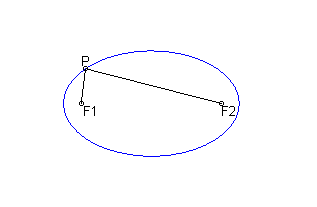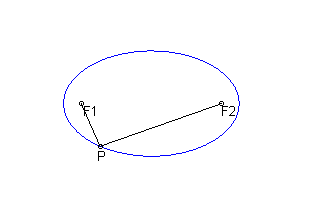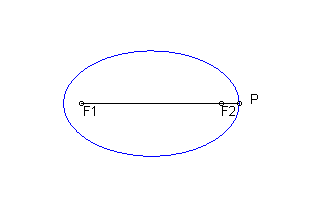
The shape of an ellipse is determined by the positions of the focus points (foci).
The shape of an ellipse is determined by the positions of the focus points (foci).

A circle is a special ellipse in that the foci are placed upon one another at the same point. This causes the radius of the orbiting body to be a constant distance from the center of the ellipse.

Note

There does not need to be a physical object at both foci in order for an object to orbit in an ellipse. One focus is the more massive object, while the second point is a mathematical construct which aids in defining the orbital motion.

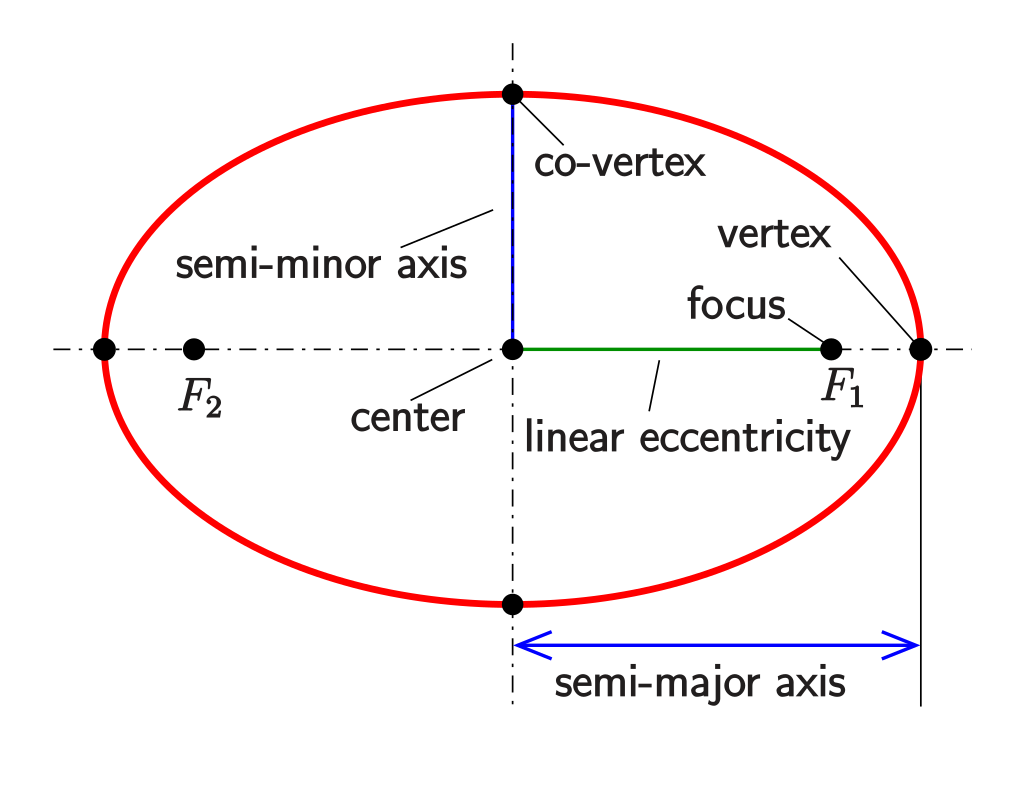
Definitions#

perihelion \(r_1\) - the closest approach to the massive body (centered upon one focus point)

aphelion \(r_2\) - the furthest distance from the massive body (centered upon one focus point)

eccentricity \(e\) - a percentage from 0 to 1 representing the roundness of an orbit. A 0 represents a perfect circle, while a 1 represents an ellipse compressed into a line.

semimajor axis \(a\) - half the distance of the major axis - a line stretching from perihelion to aphelion. Essentially, half the length of the longest axis of an ellipse.

semiminor axis \(b\) - half the distance of the minor axis. The minor axis is equal to the major axis when eccentricity is 0, and decreases to 0 as e approaches 1.

The major and minor axis define the shape of the ellipse. The minor axis is determined by the eccentricity of the orbit. The prefix
The major and minor axis define the shape of the ellipse. The minor axis is determined by the eccentricity of the orbit. The prefix "semi" just cuts an axis in half.

Setting up the equations#

Data for 1P/Halley from Mou, J. & Webster, I. (2021). 1P/halley. Comet 1P/Halley. Retrieved July 5, 2022, from spacereference.org

perihelion: 0.59 AU

aphelion: 35.07 AU

eccentricity: 0.9671

The unit AU stands for astronomical unit (the Sun to Earth distance). One AU is \(1.496\times 10^{-11}\) meters. The eccentricity is a percentage and has no units.

From this information, we can derive the semimajor axis, which is the average of the perihelion and aphelion.

\(a=\frac{r_1+r_2}{2}\)

\(a=2.667\times 10^{12}\; m\)

Next, we can derive the semiminor axis, using the semimajor axis and eccentricity.

\(b=a\sqrt{1-e^{2}}\)

Note that when the eccentricity is 0 (the ellipse is a circle) b=a indicating that there is no need to distinguish axes. When the eccentricity is 1 (an ellipse flattened to a line) b=0, as you would expect with no vertical dimension.

\(b=a\sqrt{1-e^{2}}\)

\(b=(2.667\times 10^{12})\sqrt{1-0.9671}\)

\(b=6.796\times 10^{11}\; m\)

We can now place the two foci of the ellipse using \(c=\sqrt{a^{2}-b^{2}}\) where the foci are at \((-c,0)\) and \((c,0)\), when the ellipse is centered upon the origin.

The period of the orbit is calculated using an equation derived from Kelpler's 3rd Law of Planetary Motion: "The squares of the orbital periods of the planets [or the comets] are directly proportional to the cubes of the semi-major axes of their orbits."

\(T=2\pi\sqrt{\frac{a^{3}}{\mu}}k\)

where \(k\) is a conversion factor to convert seconds to years \(k=\frac{1}{3600\times 24\times 365}\) and \(\mu\) is the universal gravitational constant \(G\;(6.67\times 10^{-11})\) times the mass of the body \(M\) at one of the focus points of the ellipse. In the case of 1P/Halley, the massive body is the sun: \(M=1.989\times 10^{30}\) kg.

\(T=2\pi\sqrt{\frac{a^{3}}{\mu}}k\)

\(a^3=1.898\times 10^{37}\)

\(\mu=MG==1.328\times 10^{20}\)

\(k=\frac{1}{3600\times 24\times 365}=3.171\times 10^{-8}\)

\(T=2\pi\sqrt{\frac{1.898\times 10^{37}}{1.328\times 10^{20}}}3.171\times 10^{-8}\)

\(T=75.332\)

Using our calculation for the semimajor axis \(a\), two constants \(GM\), the radians of a circle \(2\pi\), and a time conversion factor \(k\) we have calculated an orbital period of \(75.3\) years.

We are now ready to parametrize the ellipse equation to create a simplified orbital model.

\(x=a\cos t\)

\(y=b\sin t\)

\(0<t<2\pi\)

.. note:: The parameter t is not the angle subtended by the point with the origin. The same point on the ellipse with a different eccentricity would actually produce a different angle. The t only represents a point on the ellipse defined by x and y.

Model of 1P/Halley#

Notice the high eccentricity shown in this DESMOS model. You can click "edit graph in desmos" in the lower right and try moving the eccentricity (E) slider from 0 to 1.