Part 1: Measuring light#
Observing the unobservable#
The first step of the scientific method is observation. But how can you investigate an object or process you cannot observe. For instance, the hour hand on a clock moves too slowly to see, but you can use scientific inquiry to measure its rate of movement relative to the numbers, and make a precise prediction about where it will be after 24 hours. Likewise, subatomic particles are too small to observe in any traditional sense. Yet the streamers from their movements in a bubble chamber allows a researcher to make inferences about their properties. Computer models manipulate a range of variables to try to match the model to a complex natural phenomenon, often applying known principles from other contexts. The concept of "observation" is expanded in modern science.
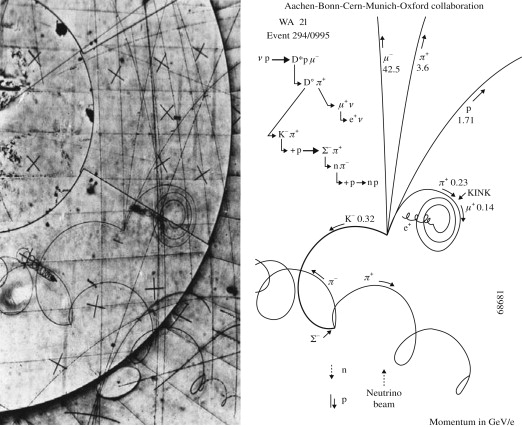
Determining the properties of stars is a similar process. It isn't possible at present to visit a distant star and take direct physical measurement. It simply appears to be a twinkling point in the night sky, even under high magnification.
Luminance#
The units and concepts related to light can be quite a tangle to unweave, but there is sound logic to it.
Brightness, or luminous intensity, is typically measured in candela per square meter \(\frac{cd}{m^2}\) - the intensity of light falling on a surface. Or more specifically, it is a measurement of the amount of visible light emitted or reflected per unit area.
In the context of light bulbs, the measurement is called luminous flux. The unit is lumen lm. This measurement of light accounts for all visible light emitted from a source in every direction (not only a particular surface like luminous intensity). A lumen is based on human perception of light, so the invisible portions of the electromagnetic spectrum are not included in this measurement.
A similar concept is illuminance. The unit for this value is lux lx. Like brightness in \(\frac{cd}{m^2}\), lux measures the amount of light falling on a surface, but in terms of lumen per square meter \(\frac{lm}{m^2}\). The important difference here is that \(\frac{cd}{m^2}\) measures perceived brightness, while lux measures actual brightness. One way to visualize the difference is to imagine a person inside a car, and another person outside a car, measuring different brightness levels (candela per square meter) on their retinas; yet the headlight objectively emits a constant lux value.

Radiance#
It is also possible to evaluate light using energy measurements - or more specifically the power of energy (Joules per second) in watts W. This is called radiant flux. It is an objective measurement of the power of light (radiant energy) emitted from a source in all directions. Radiant flux contains all electromagnetic radiation, including visible light, infrared, ultraviolet, radio, x-rays, and gamma radiation.
Applied to a surface, the measurement is called irradiance or flux density - measured in Watts per square meter \(\frac{W}{m^2}\). This is the radiant energy incident on a surface. It is separate from radiance, which measures the radiant energy emitted from a source - and is measured in Watts per square meter per steradian \(\frac{W}{m^2\cdot sr}\).
Note
A steradian (Greek "stereos" or solid radian) is like an angle subtended on a circle (slice of pie), but in three dimensions. A steradian slices out a piece of a sphere which is the square of the radius. For instance, a sphere with a 3 meter radius would have 9 steradians. The surface area of the entire sphere would be \(4\pi r^2=4\pi 9\approx 113.1\). The surface area of one steradian would be \(\frac{1}{9}\cdot 113.1\approx 12.56\) or \(4\pi\). The steradian measurement scales with the radius of the sphere, so it doesn't change with distance.
Classifying light measurements#
| total energy emitted | light falling on a surface | subjective to human eye |
|---|---|---|
| luminous flux lm | illuminance lx | brightness \(\frac{cd}{m^2}\) |
| radiant flux W | irradiance \(\frac{W}{m^2}\) | |
| radiance \(\frac{W}{m^2\cdot sr}\) |
| visible light | all light |
|---|---|
| brightness \(\frac{cd}{m^2}\) | radiant flux W |
| luminous flux lm | irradiance \(\frac{W}{m^2}\) |
| illuminance lx | radiance \(\frac{W}{m^2\cdot sr}\) |
| Luminance | Radiance | Luminosity |
|---|---|---|
| luminous intensity | radiant flux | luminous flux |
| illuminance | irradiance |
Short definitions#
Brightness: A subjective term used to describe the overall perception of how bright a source of light appears to the human eye.
Luminous flux: A measure of the total amount of visible light emitted by a source, measured in lumens lm.
Illuminance: A measure of the amount of light falling on a surface, measured in lux lx.
Radiant flux: A measure of the total amount of energy emitted by a source, measured in watts W.
Irradiance: A measure of the radiant flux incident on a surface, measured in watts per square meter \(\frac{W}{m^2}\). Also called flux density. Sometimes the variable E is used to describe this value.
Radiance: A measure of the intensity of light emitted by a surface, measured in watts per square meter per steradian \(\frac{W}{m^2\cdot sr}\)
Inverse square law#
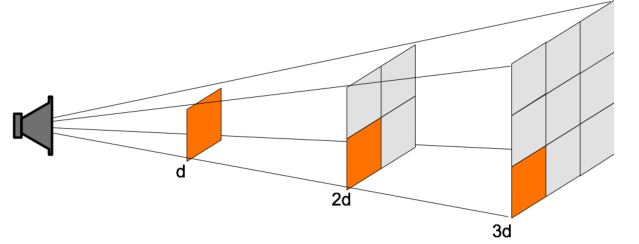
Light from a point source spreads out as it moves away from the source. You can envision it like spokes of a bicycle wheel growing less dense toward the rim. Fewer spokes equates to lower intensity radiation. The equation which describes it is:
\(E=\frac{P}{4\pi r^2}\)
where E is irradiance measured in \(\frac{W}{m^2}\), \(P\) is radiant flux (total power emitted from source in watts) and \(4\pi r^2\) is the surface area of a light sphere of radius \(r\).
It is important to note that \(r\) here is not the radius of the star, but the radius of the light sphere. In other words, \(r\) is the distance from the star to the observer. The equation depends upon knowing this distance and the radiant flux of the light source.
As an example, plugging in the solar flux of the Sun and using the distances from the Sun to Earth, Mars, Jupiter, and Saturn gives the following chart in Excel.

The power curve equation returned by Excel is \(y=\frac{1351.1}{r^2}\). We can use this to explore the inverse square law.
| distance r | \(\frac{1351.1}{r^2}\) | ratio to 1 |
|---|---|---|
| 1 | 1351.1 | 1 |
| 2 | 337.775 | 0.25 or \(\frac{1}{4}\) |
| 5 | 54.044 | 0.04 or \(\frac{1}{25}\) |
| 10 | 13.511 | 0.01 or \(\frac{1}{100}\) |
As the name implies, observe that the irradiance falls off as the inverse square of the distance. This, of course, may be obvious from the original equation, which can be rewritten like this: \(E=\frac{P}{4\pi}\cdot \frac{1}{r^2}\)
Or in the specific scenerio above as:
\(E=3.024\times 10^{26}\cdot \frac{1}{r^2}\). Notice that this is simply a constant multiplied by the inverse square of the distance - the constant being the radiant flux of the star over \(4\pi\)
Magnitude#
Magnitude is an old idea (130 BC by Hipparchus) which organizes light in terms of the inverse square law. It is a measure of apparent brightness compared to a reference star, usually Vega.

Brightness of a star can be measured with a photometer, a bolometer, or a CCD camera.
Note
Photometers can be used to measure the brightness of a star in different parts of the electromagnetic spectrum, while bolometers measure the total energy (or thermal radiation) emitted by an object by converting incoming energy into heat, and then measuring the increase in temperature. Bolometers are better for detecting very faint or cool objects, and photometers are better for stars. CCD cameras are very sensitive and offer high resolution, but suffer from noise.

On the other hand, radiometers measure the flux density of radiant energy, as a measure of light intensity. The flux can refer to different types of energy, so it can be measured in a few different ways, including:
\(\frac{W}{m^2}\) or \(\frac{J}{m^2}\) or \(\frac{erg}{cm^2\cdot s}\)
Note
The last set of units uses an erg - a unit representing the small amount of energy required to move one gram at the speed of one cm per second. The collection of units in \(\frac{erg}{cm^2\cdot s}\) is specifying how many ergs are passing through one square cm in one second.

With this data we can compare star brightnesses with one another, The problem is, some objects are extraordinarily bright and others vanishingly dim. In practice, we wouldn't be saying the Sun is something like 10 times or 100 times brighter than the star Vega; we would be noting it is 50,000,000,000 times brighter. Using such big numbers gets tedious, so we introduce a logarithmic scale.
\(\phi=2.512^{-m}\)
This equation compares flux \(\phi\) with magnitude \(m\) in such a way that 5 levels of magnitude are equivalent to 100 times the flux. But they are inversely proportional, so that decreasing 5 magnitudes, increases the flux by 100 times.
| mag | E |
|---|---|
| -3 | 15.85108 |
| -2 | 6.310144 |
| -1 | 2.512 |
| 0 | 1 |
| 1 | 0.398089 |
| 2 | 0.158475 |
| 3 | 0.063087 |
| 4 | 0.025114 |
| 5 | 0.009998 |
| 6 | 0.00398 |
| 7 | 0.001584 |
Notice that at \(m=0\), \(\phi=1\) and at \(m=5\), \(\phi=0.009998\). Rounding errors aside, \(0.01\) is \(\frac{1}{100}\) of \(1\). Increasing the magnitude by 5, decreases the flux by 100 times.
This magnitude scale tells us nothing about how bright a star is intrinsically. It could be bright and far away, or dim and close. There is no way to know unless we can determine how far away it is. See Part 2: Measuring stellar distances for information about how to do this.
Also see Part 3: Practical measurements of flux to learn more about fluxes used in practice in Astronomy.
Note about Magnitudes#
Pogson magnitudes and asinh magnitudes are both ways to measure the brightness of astronomical objects, but they use different mathematical formulas to do so.
Pogson magnitudes:
\(m = -2.5 \times log_{10}(\phi) + C\)
where m is the Pogson magnitude, flux is the measured flux of the object, and constant is a zero-point offset. T
Hyperbolic sine magnitudes:
\(m = \frac{-2.5}{\ln(10)} \times \left(asinh(\frac{\phi}{b}) + \ln(b)\right)\)
where m is the asinh magnitude, flux is the measured flux of the object, b is a constant that scales the flux (usually created to match the Pogson magnitudes), and asinh is the inverse hyperbolic sine function.