Part 2: Measuring stellar distances#

Distance to nearby stars with parallax#

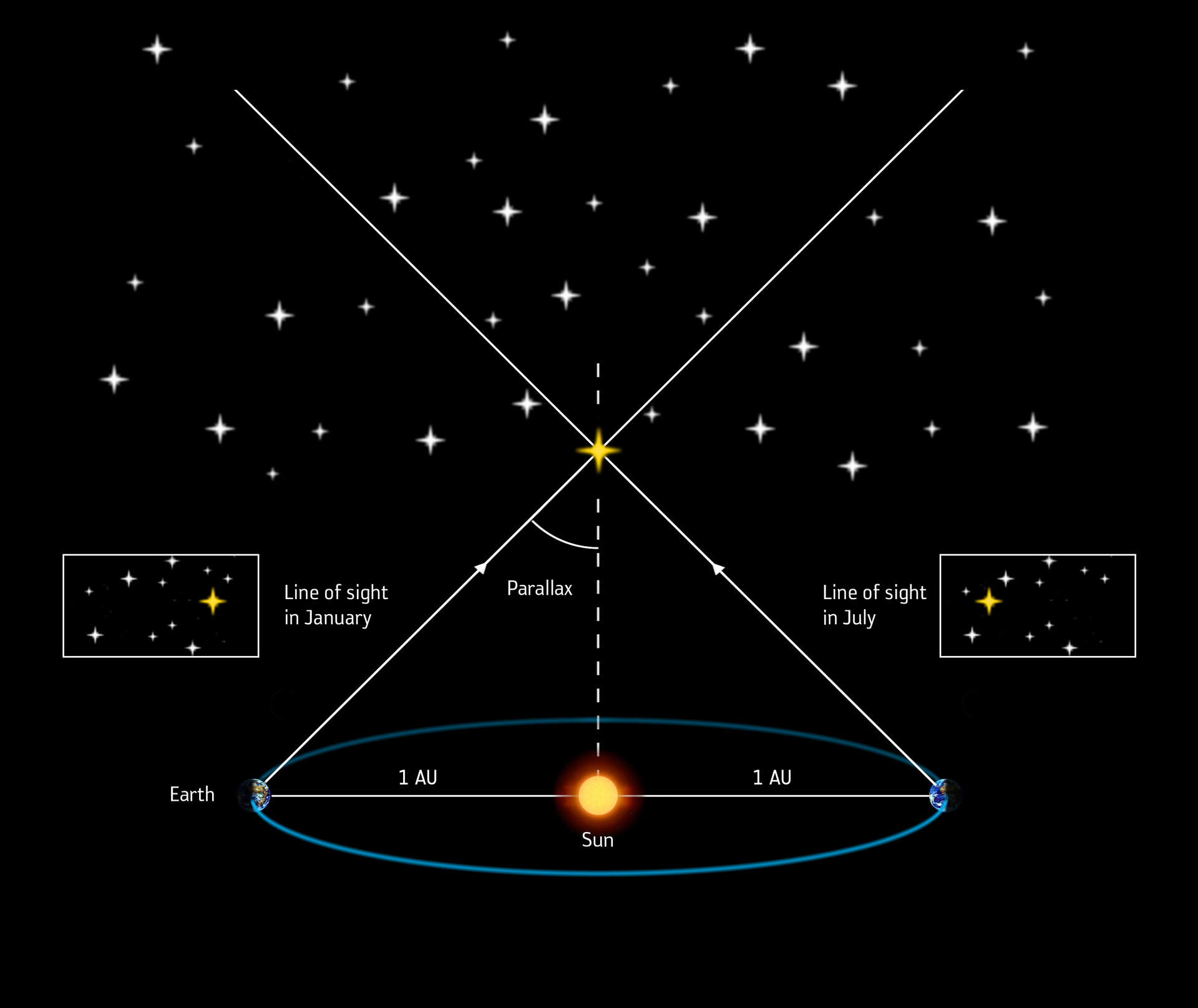
Image from stellar parallax: From ESA 2021 - https://www.esa.int
Image from stellar parallax: From ESA 2021 - https://www.esa.int

It is possible to use parallax to determine how far away a star is. For instance, the star Rigel, in the constellation of Orion, moves 0.00000105 degrees from July to January, against the background stars. It isn’t a large angle, but it is enough to calculate the distance with trigonometry.

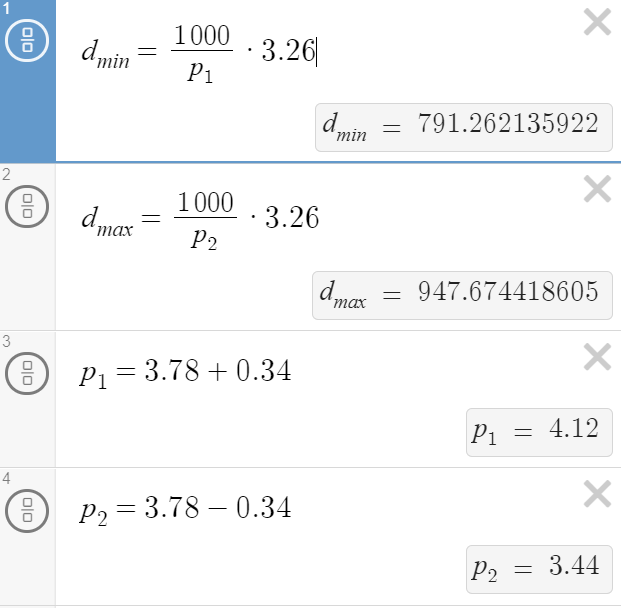
The relation is that the distance in parsecs (3.26 light years) is equal to the inverse of the parallax shift in milliarcseconds: \(d_{pc}=\frac{1000}{p_{mas}}\)

Normally degrees are too large an angle to use effectively in Astronomy, so star catalogues use milliarcseconds. One degree is 60 arcminutes or 3600 arcseconds, and there are 1000 milliarcseconds in one arcsecond. In other words, one degree is equal to 3.6 million milliarcseconds.

A quick search in SIMBAD (Set of Identifications, Measurements and Bibliography for Astronomical Data), run by Strasbourg Astronomical Data Center (CDS), you find that Rigel has a parallax measurement (taken in 2007) of: 3.78 +/- 0.34 mas.

The parallax of Rigel is 3.78 +/- 0.34
The parallax of Rigel is 3.78 +/- 0.34

Multiplying by 3.26 to get the light year distance, you obtain the following distance range for Rigel:

The distance to Rigel is between 791 and 948 light years.
The distance to Rigel is between 791 and 948 light years.

As effective as this technique may be, it is of no use for distant stars or galaxies. Parallax only works out to about 10 pc for ground-based telescopes to 100 pc for space-based instruments, like Hubble and Gaia. For comparison, the nearest galaxy is 765,000 pc.

Distance to galaxies with the Doppler effect#

When a motorcycle passes you, you hear a rising pitch, followed by a falling pitch after it passes. The equation which demonstrates this phenomenon is:

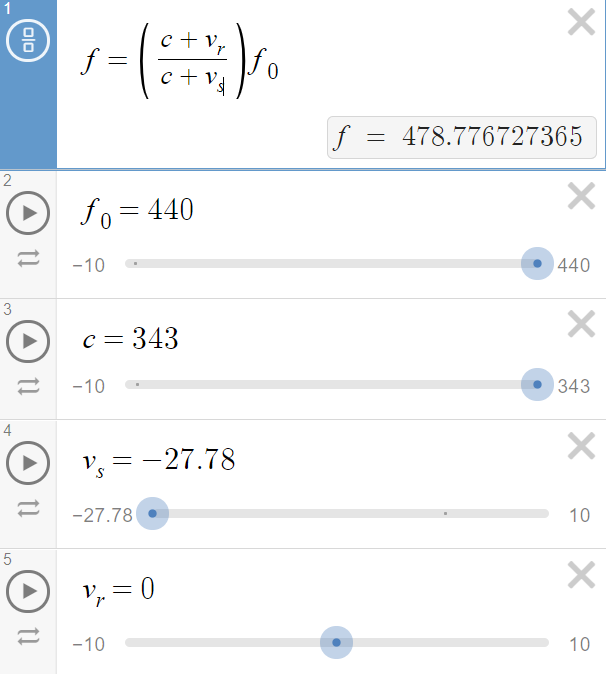
\(f=\left(\frac{c+v_{s}}{c+v_{r}}\right)f_{0}\)

where c is the speed of the medium (in this case, the speed of sound at 343 mps), v_r is the velocity of the receiver, v_s is the velocity of the source, f_0 is the true frequency of the source and f is the frequency perceived by the receiver. Whether you add or subtract the velocity of the source or receiver depends upon the direction of the sound. In the case of a receiver at rest, listening to a frequency source approach, the velocity sign would be negative. The sign is positive when the source is moving away.

If the motorcycle is traveling at 100 kph (27.78 mps), and making a hum at 440 Hz, the equation would look like this:

The 440 Hz frequency rises to ~479 Hz as the motorcycle approaches
The 440 Hz frequency rises to ~479 Hz as the motorcycle approaches

Note

Technically, unless you were in the street with the motorcycle coming right at you, you would need to add a small variable to v_s which indicated your angle to the source: \(v_{s}=-27.78\cos\left(A\right)\).

The light we see ranges from about 380 nm (violet light) to 700 nm (red light) to produce the colors of the rainbow.
The light we see ranges from about 380 nm (violet light) to 700 nm (red light) to produce the colors of the rainbow.

The corresponding frequencies are found with \(ν=\frac{c}{λ}\). Astronomers apply the same principle to the light of moving stars. Let's look at a simple example.

Question

Suppose a source of pure green light at the wavelength 550 nanometers is moving away from you at 1/10th the speed of light. How would its frequency change?

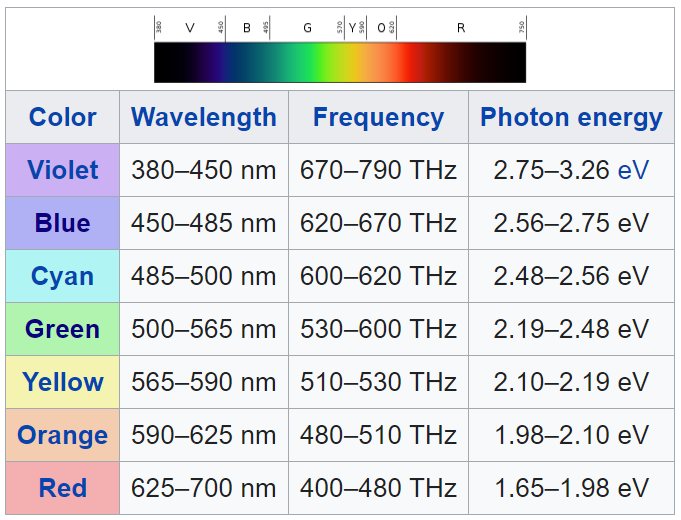
Notice that the shorter wavelengths produce blues and violets and the longer wavelengths produce oranges and reds. To calculate the light's frequency just divide it by the speed of light \(λ=\frac{c}{ν}\) By the way, the \(ν\) here is the Greek character nu - and is the variable for frequency, not velocity.

Therefore, the frequency of 550 nm green light is 545 THz:

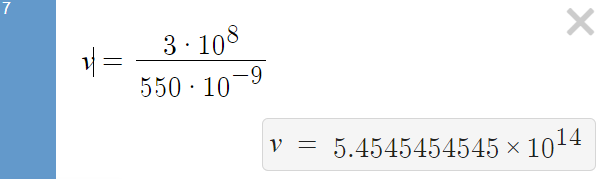
550 nm light has a frequency of 545 THz
550 nm light has a frequency of 545 THz

We can use the known velocity and frequency of the source to calculate the shift in frequency (and wavelength) observed by the receiver.

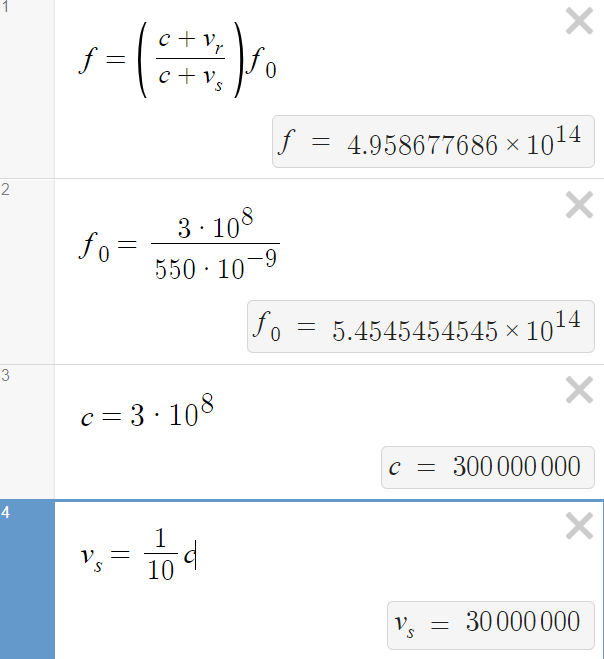
The green light frequency dropped from 545 THz to 496 Thz
The green light frequency dropped from 545 THz to 496 Thz

The green light frequency fell from 545 THz to 496 Thz. This frequency shift corresponds to a wavelength shift from 550 nm to 605 nm. As the frequency drops, the wavelength increases, toward to the red end of the spectrum. This is the so-called redshift.

This would mean that the green color below, when moving away from you at one-tenth light speed, would appear to be this orange color.

550 nm light at rest
550 nm light at rest
550 nm light moving at 0.1c appears to be 605 nm light
550 nm light moving at 0.1c appears to be 605 nm light

Astronomers use the known spectral lines of hydrogen to determine how much shift is present in the spectrum of a galaxy, and use this information to determine its radial velocity and distance. Read Stellar Redshift for more information.