How far away are galaxies?#
The Great Debate#
People used to believe that galaxies were nebulae just outside the Milky Way. With the development of more sophisticated telescopes, it became clear that many of these "nebulae" had spiral structures like our own galaxy. Harlow Shapley, head of the Harvard College Observatory, and Heber Curtis, president of the Astronomical Society of the Pacific, held a debate about the nature of these stuctures on April 26, 1920 - at the Smithsonian Museum of Natural History in Washington D.C.
Shapley tried to demonstrate that the Milky Way was the entire universe. His primary argmunt was that if the Pinwheel Galaxy were extragalactic, and roughly the same size as our galaxy, it's small apparent size would put it at least 100 million light years away. He assumed this was a ridiculous distance, and rejected it. It's actual distance is 20 million light years; and it is 70% larger than the Milky Way. But few scientists of the time would accept distances in the millions of light years.
Curtis, on the other hand, noted the number of nova detected in the Pinwheel galaxy - far more than the average within the Milky Way. Why would one tiny section of the universe have a much higher frequency of exploding stars? He argued it was because the Pinwheel galaxy was an "island universe" very distant from our own.
The result of the debate was undecided until Edwin Hubble settled it by examining variable stars, and demonstrating that "galactic nebulae" were not nebulae at all, but distant galaxies, similar to our own.
Cepheid Variables#
Henrietta Swan Leavitt, who worked at Harvard College Observatory, discovered Cepheid variables in 1912. Variables are stars which increase and decrease in brightness over a regular period. This phenomenon was well known at the time. What Leavitt discovered was that, in a particular variety of variable, the brightest stars pulsed over a longer period. These were named Cepheid variables, named after the constellation Cepheus.
This was a breakthrough; but a piece of the puzzle was still missing. Because she found these variable stars in the Large and Small Magellanic clouds (now known to be galaxies), she inferred that they were all a similar distance away. But that distance was unknown at the time. For the relationship to be useful, there needed to be a parallax measurement of a similar star (read Measuring stellar distances to learn about using parallax to measure distances). This was soon accomplished.
But the correlations to Milky Way cepheids, from which parallax measurements are possible, were of low quality - a victim of high errors. However, in 2007, a sharp calibration was obtained from the Hubble Space Telescope data. With all the data collected and analyzed it was possible to generate the following function:
\(M=(-2.43\pm{0.12})(\log_{10} P-1)-(4.05\pm{0.02})\)
where \(P\) is the period in days and \(M\) is the mean absolute magnitude
This calibrated formula can be used to find the distances to classical cepheid variables in other galaxies.
Calculations with a classic cepheid variable within the Milky Way#
To use an example, the star Delta Cephei is found within the Milky Way. Its trigonometric parallax is measured at \(3.77\pm0.16\) mas (milliarcseconds). This corresponds to a distance from:
\(\frac{1}{0.00393}= 254\; parsecs=828\; light \;years\)
to:
\(\frac{1}{0.00361}= 277\; parsecs=904\; light \;years\)
The star pulsates in a cycle of 5.366249 days from 3.48 magnitude to 4.37 magnitude (apparent brightness).
Next we determine its absolute magnitude according to the Hubble model
\(M=(-2.43\pm{0.12})(\log_{10}P-1)-(4.05\pm{0.02})\)
Here are the mean, min and max absolute magnitude for the star Delta Cephei.
\(M=(-2.43)(\log_{10}(5.366249)-1)-(4.05)=-3.93910009395\)
Using the Hubble model uncertainty, the cepheid's mean magnitude may be anywhere from -3.45 to -3.34 (the lower the number, the brighter the star). We now have an apparent magnitude, an absolute magnitude, and a period. Our distance was determined by parallax.
Because we know the apparent and absolute magnitudes (the actual brightness from 10 parsecs) we can calculate the distance in a way other parallax.
\(d=10^\frac{(m-M+5)}{5}\)
\(d=10^\frac{(3.48+3.45+5)}{5}=243\;pc=792.6\;ly\)
\(d=10^\frac{(4.37+3.34+5)}{5}=348\;pc=1135\;ly\)
| distance calculation | min | mean | max |
|---|---|---|---|
| parallax | 828 | 866 | 904 |
| cepheid | 793 | 964 | 1135 |
While these mean distances are not precisely equal, when you add more and more cepheids to a plot of parallax distance to cepheid distance, you can observe a trend line running through the points. This allows astronomers to use the same reasoning with cepheids in other galaxies - stars much too far away to use parallax to calculate distance.
Calculations with a classic cepheid variable outside the Milky Way#
Convinced that our Hubble model works, we can seek to determine how far away a sample extragalactic object might be.
First we find some cepheid variable stars in an extragalactic object and measure its period and apparent magnitude. Let's use a few cepheids found in the globular cluster NGC 1866, and use them to estimate its distance.

I will pull a few cepheids from a study reported by the Royal Astronomical Society (Marconi et al., 2016).
| ID | Period in days | Visual band magnitude |
|---|---|---|
| V6 | 1.944262 | 16.18 |
| V8 | 2.007 | 16.19 |
| HV12199 | 2.63916 | 16.29 |
| HV12200 | 2.72498 | 16.16 |
| New | 2.94293 | 16.17 |
| HV12203 | 2.95411 | 16.14 |
| We8 | 3.039849 | 16.14 |
| We3 | 3.04904 | 15.99 |
| WS11 | 3.0533 | 16 |
| We2 | 3.05485 | 16.01 |
| V1 | 3.08455 | 16.13 |
| HV12202 | 3.1012 | 16.1 |
| HV12197 | 3.14371 | 16.11 |
| We6 | 3.28994 | 15.99 |
| V4 | 3.318 | 16.1 |
| V7 | 3.45207 | 16 |
| HV12198 | 3.5228 | 15.98 |
| - |
We have the period and mean visual magnitude, so we can use the Hubble model to determine the absolute magnitude of each cepheid.
- \(ID\) is the identification of the cepheid
- \(P\) is the period in days
- \(M_v\) is the apparent magnitude in the visual band
- \(M_{abs}\) is the calculated absolute value using the Hubble model \(M=(-2.43\pm{0.12})(\log_{10}P-1)-(4.05\pm{0.02})\)
- \(DM\) is distance modulus, which is \(m-M\) (apparent magnitude - absolute magnitude)
- \(pc\) is the calculation of the distance in parsecs \(d=10^\frac{(m-M+5)}{5}\)
- \(ly\) is the calculation of the distance in light years \((3.26d)\)
| ID | P | M_v | M_abs | DM | pc | ly |
|---|---|---|---|---|---|---|
| V6 | 1.944262 | 16.18 | -2.32 | 18.5 | 50,157 | 163,513 |
| V8 | 2.007 | 16.19 | -2.36 | 18.55 | 51,173 | 166,823 |
| HV12199 | 2.63916 | 16.29 | -2.64 | 18.93 | 61,211 | 199,549 |
| HV12200 | 2.72498 | 16.16 | -2.68 | 18.84 | 58,558 | 190,899 |
| New | 2.94293 | 16.17 | -2.76 | 18.93 | 61,070 | 199,088 |
| HV12203 | 2.95411 | 16.14 | -2.76 | 18.9 | 60,343 | 196,718 |
| We8 | 3.039849 | 16.14 | -2.79 | 18.93 | 61,188 | 199,473 |
| We3 | 3.04904 | 15.99 | -2.8 | 18.79 | 57,188 | 186,432 |
| WS11 | 3.0533 | 16 | -2.8 | 18.8 | 57,491 | 187,420 |
| We2 | 3.05485 | 16.01 | -2.8 | 18.81 | 57,770 | 188,331 |
| V1 | 3.08455 | 16.13 | -2.81 | 18.94 | 61,340 | 199,970 |
| HV12202 | 3.1012 | 16.1 | -2.81 | 18.91 | 60,657 | 197,743 |
| HV12197 | 3.14371 | 16.11 | -2.83 | 18.94 | 61,342 | 199,975 |
| We6 | 3.28994 | 15.99 | -2.88 | 18.87 | 59,341 | 193,451 |
| V4 | 3.318 | 16.1 | -2.89 | 18.99 | 62,682 | 204,345 |
| V7 | 3.45207 | 16 | -2.93 | 18.93 | 61,025 | 198,941 |
| HV12198 | 3.5228 | 15.98 | -2.95 | 18.93 | 61,064 | 199,070 |
| Mean | 2.96 | 16.1 | -2.75 | 18.85 | 59,035 | 192,455 |
From this sample of cepheids from NGC 1866, we have derived an average distance modulus of 18.85 and a mean distance of 192,000 light years.
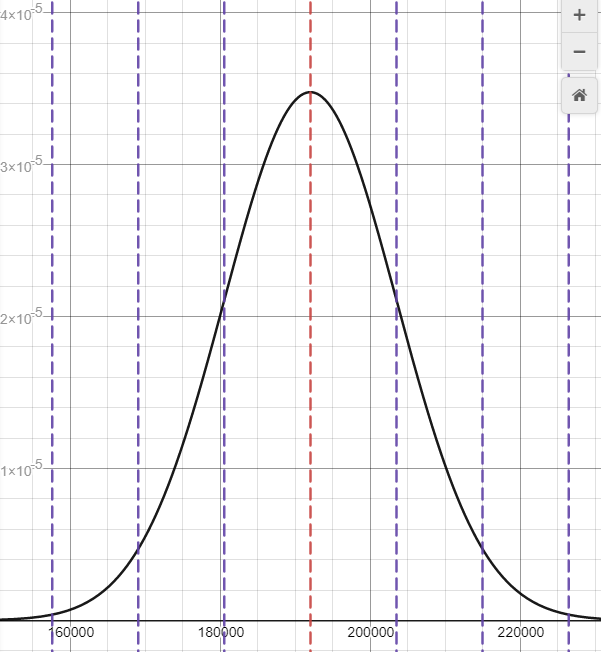
How do our quick calculations stack up against professional estimates?
Result
"Hubble Space Telescope V,I photometry of stars in the Large Magellanic Cloud Cluster NGC 1866 shows a well defined cluster main sequence down to V=25 mag, with little contamination from field or foreground stars. We use the main sequence fitting procedure to link the distance of NGC 1866 to the Hipparcos determination of the distance for the Hyades MS stars, making use of evolutionary prescriptions to allow for differences in the chemical composition. On this basis we find a true distance modulus for NGC 1866 of 18.35 +/- 0.05 mag. If the cluster is assumed to lie in the LMC plane then the LMC modulus is 0.02 mag less" (Walker, 2001).
| Compared | DM | pc | ly |
|---|---|---|---|
| Our calculations | 18.85 | 58884 | 191963 |
| Astrophysical Journal | 18.35 | 46774 | 152482 |
We are close with the distance modulus, but the calculated distances are very sensitive to small changes. Still, considering our selection criteria for cepheids was random, and the fact that we didn't account for any controls, this is quite a strong result. These values are within the same order of magnitude, and definitively show that this globular cluster is not within the Milky Way Galaxy.

Created in Space Engine
References#
Marconi M., Raimondo G., Brocato E., Molinaro R., Ripepi V., Carini R., Coppola G., Walker A. R., Welch D. L. (2016). The Cepheids of NGC 1866: a precise benchmark for the extragalactic distance scale and stellar evolution from modern UBVI photometry, Monthly Notices of the Royal Astronomical Society, Volume 457, Issue 3, Pages 3084–3095.
Walker, A. R., Raimondo, G., Di Carlo, E., Brocato, E., Castellani, V., & Hill, V. (2001). The Distance of the Large Magellanic Cloud Cluster NGC 1866. The Astrophysical Journal, 560(2), L139.