An exploration of SI units: Part I - Mechanics#

---

Universal science units are referred to as SI units, after the French expression: Le Système International d'Unités. The system, as it is now used, solidified in 1960 in Sèvres, France - close to Paris, under the umbrella of CGPM, Conférence Générale des Poids et Mesures. Despite the French name, the conference was the international effort of 51 member states, including all developed nations.

Mechanics units without Calculus#

---

Let’s begin with some units used in mechanics. Imagine moving a chest of drawers across the floor. You need to use a force to move the furniture some distance. The more force you exert, the more work is required of you. The further you move the furniture, the more work is required of you.

\(W=Fs\)
Work = Force \(F\) times the displacement from the starting position \(s\).

What is the unit for work? Work is a use of energy; it is the same unit as energy – Joules (J).

To push the furniture requires energy. Let’s look at energy and force more closely. Energy is measured in Joules. Force is measured in Newtons. Think about what you do when you push the chest of drawers. You are accelerating a mass. Therefore, Force is equal to mass times acceleration.

\(F=ma.\)

Mass is measured in kg and acceleration is changing an object’s velocity over time, or \(\frac{v}{t}\). Velocity is measured in meters/second, so acceleration is \(\frac{\frac{m}{s}}{s}\). But that is an awkward compound fraction; it is the same thing as \((\frac{m}{s})(\frac{1}{s})\). Therefore, \(\frac{\frac{m}{s}}{s}=(\frac{m}{s})(\frac{1}{s})=\frac{m}{s^2}\). Since force is \(F=ma\), then the base units for force (Newtons) are \(kg\cdot \frac{m}{s^2}\).

What base units do we use for energy – for Joules?
Moving the chest of drawers required us to use force to move it some distance \(W=Fs\), therefore Joules = Newtons \(\cdot\) meters (\(J=Nm\)). Since we now know that Newtons are \(kg\cdot\frac{m}{s^2}\), we just multiply that by the distance we have pushed the dresser in meters: \(kg\cdot\frac{m}{s^2}\cdot m=\frac{kg\cdot m^2}{s^2}\)

To move the dresser, we accelerate a mass over a distance (force), to perform work (energy).

Pressure#

---

How much pressure are we putting on the dresser?

Pressure depends upon surface area. For instance, if we use a telephone book and a needle to place the same force on a piece of paper, the needle will pierce the paper; the telephone book will not. The needle exerts more pressure. Same force; much different pressure. The smaller the surface area, the greater the pressure. Pressure is measured in Pascals.

\(P=\frac{F}{A}\)

\(P=\frac{\frac{kg \cdot m}{s^2}}{m^2}\)

\(P=\frac{kg \cdot m}{m^2 \cdot s^2}\)

\(P=\frac{kg}{m \cdot s^2}\)

To calculate pressure, we need force and area. Area is given. However, area is given in \(cm^2\) and we need \(m^2\).

\(4\;cm\cdot 1\;cm\cdot \frac{1\;m}{100\;cm}\cdot \frac{1\;m}{100\;cm}=\frac{4}{10000}=0.0004 \;m^2\)

Force is mass times acceleration, therefore we can calculate force with the given information:

\(F=ma\)

\(F=68\;kg\cdot 9.81\;\frac{m}{s^2}\)

\(F=667.08\;N\)

\(P=\frac{F}{A}=\frac{667.08\;N}{0.0004 \;m^2}=1,667,000\;Pa\;or\;1.667\;MPa\;\)

This sounds like a lot of force, but for comparison, this is approximately 242 psi or 1.5 times the pressure of a human bite. We can check our work in Wolfram Alpha.

Mechanics units with Calculus#

---

Things change a bit if the components of our functions don't remain constant. Of course, this is mostly what you will find in the real world, meaning you must eventually learn to use Calculus in order to apply Physics. We will use only one example here \((W=Fs)\), but the concepts apply generally to other formulas in Physics.

We have seen that work is a force exerted over a distance; however, this equation is suitable only for the particular case where the force is applied on a straight line path and the force is constant. What if these constraints are not the case?

Let's assume you are pushing the dresser in a constant direction, along a line, but that the force you exert is variable. We will define a displacement from \(a\) to \(b\) meters, from when we start moving the furniture until we stop. The force we exert is defined by the function F(s). In other words, we define the force by the distance we move. That may seem kind of backwards, but we do it this way because force is measured along the y-axis and displacement along the x-axis. From these definitions we get the equation:

\(W=\int_{a}^{b} F(s)\cdot ds\)

The integration symbol, which looks like an extended S, means sum - particularly the sum of all the force measurements at every distance interval from a to b, with each distance interval being infinitely small. For every tiny movement ds, the force also changes. The sum of these forces, with respect to displacement, is the amount of work we have done.

Here is an example of force measured at displacement intervals.

Using regression techniques on a computer or calculator, you identify the following function with high correlation:

\(F=-300s^3+162s^2\)

Using our function, we can find the x-intercept (our starting and resting points) by setting the force equal to zero and solving for \(s\).

We can distribute out the \(s^2\) and get:

\(s^2(-300s+162)=0\)

We can split this into two equations:

\(s^2=0 \land -300s+162=0\)

Solving the first equation is trivial:

\(s^2=0\)

\(s=\sqrt{0}\)

\(s=0\)

We can simplify the second equation by factoring out constants, eliminating it by dividing both sides by the constant, then solving for \(s\):

\(-300s+162=0\)

\(-6(50s-27)=0\)

\(50s-27=0\)

\(50s=27\)

\(s=\frac{27}{50}=0.54\)

Therefore, our starting and ending distances are \(s=0\) and \(s=0.54\) meters. We can integrate our function over that interval. Using DESMOS, Matlab, Wolfram Alpha, or a calculator like the TI-84, you can skip through the integration quickly to get:

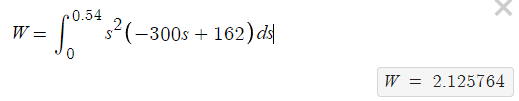
We have our answer: You have performed 2.13 Joules of work to move the dresser 0.54 meters with a variable force.

Integration by hand#

---

Here is the manual integration, if you need the mathematics practice, don't have access to technology, or just like to waste time.

First, find the indefinite integral,

\(W=\int_{0}^{0.54} -300s^3+162s^2)\cdot ds\)

\(\int -300s^3+162s^2\cdot ds\)

integrate each term in the polynomial,

\(\int -300s^3\cdot ds+\int 162s^2\cdot ds\)

factor out the constants,

\(-300\cdot\int s^3\cdot ds+162\cdot\int s^2\cdot ds\)

integrate normally,

\(-300\cdot \frac{s^4}{4}\cdot+162 \frac{s^3}{3}\)

simplify,

\(-75s^4+54s^3\)

and finally, evaluate for \(s=0\) and \(s=0.54\)

\(-75(0)^4+54(0)^3=0\)

\(-75(0.54)^4+54(0.54)^3=2.125\)

Therefore, the work performed between \(s_1=0\) and \(s_2=2.125\) is \(s_2-s_1 = 2.12\) Joules.

Units overview#

---

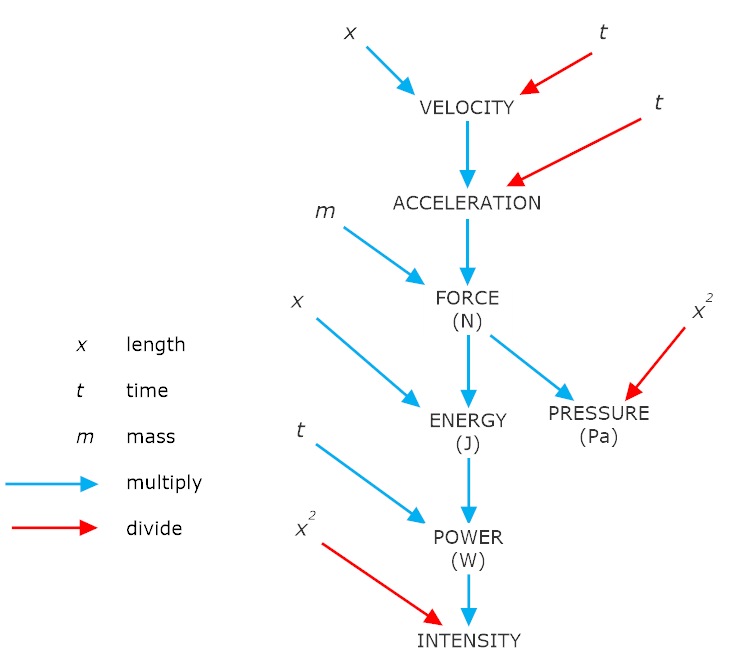
This is great organizational chart. To use it, note the color of the arrows: red is divide and blue is multiply. For instance, Force is measured in Newtons and is composed of mass times acceleration, which is in turn formed by velocity over time. Force is also a component of pressure: \(\frac{F}{x^2}\), where \(x\) is a distance unit and \(x^2\) is an area.